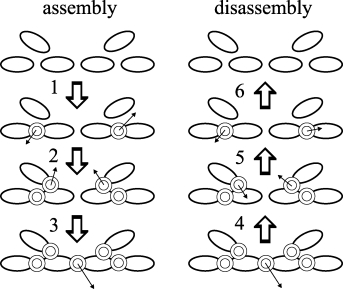
Fig.1 Concept of O(N) Forward Dynamics
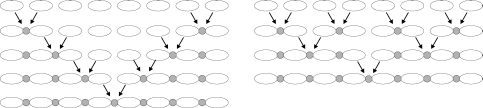
Fig.2 Example Schedules for Parallel Computation
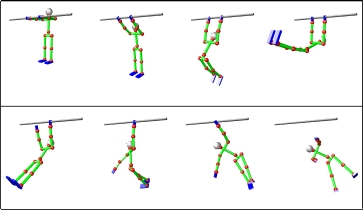
Fig.3 Simulation of a Human Figure
We developed an efficient forward dynamics algorithm applicable to any closed kinematic chains. The asymptotic complexity of the algorithm is O(N) where N is the number of links on a single processor, and the computation time is reduced down to O(logN) by parallel computation on O(N) processors.
Figure 1 illustrates the concept of the algorithm. The method cosists of the following two procedures:
- Starting from independent links without any joint constraints, add the joints one by one and compute the constraint force at each joint. Note that each constraint force is temporary value because it does not include the effect of constraints added later.
- Compute the final constraint forces by cutting the joints in the reverse order of procedure 1. The joint accelerations are also computed at this stage.
If the computations for adding/removing two joints are independent, they can be processed in parallel. We can tune the parallelism (number of independent processes) and the total computational cost by changing the order of adding the joints. Figure 2 shows two possible orders (schedules) for an eight-link serial chain. We can use up to two processors if we take the schedule in Figure 2 left, while Figure 2 right allows up to four processors. Therefore it is more efficient to use the schedule of Figure 2 right if we have more than four processors. If we have less than two processors, however, the schedule of Figure 2 left is better because the total computational cost is smaller.
Table 1 shows the time for computing the joint accelerations of serial chains with 8-32 links using 1-8 processors. Figure 3 shows several snapshots from a simulation of a structure-varying human figure. This algorithm is included in the humanoid simulator OpenHRP.
| # of processes | |||||
| 1 | 2 | 4 | 8 | ||
| # of links | 8 | 1.31 | 0.98 | 0.90 | - |
| 16 | 2.75 | 1.87 | 1.70 | 1.57 | |
| 32 | 6.08 | 3.93 | 3.34 | 2.90 | |

- K. Yamane and Y. Nakamura: "Efficient Parallel Dynamics Computation of Human Figures,'' Proceedings of International Conference on Robotics and Automation, pp.530-537, Washington DC, May 2002.
- F. Kanehiro, K. Fujiwara, S. Kajita, K. Yokoi, K. Kaneko, H. Hirukara, Y. Nakamura, and K. Yamane: "Open Architecture Humanoid Robotics Platform," Proceedings of International Conference on Robotics and Automation, pp.24-30, Washington DC, May 2002.
- K. Yamane and Y. Nakamura: "O(N) Forward Dynamics Computation of Open Kinematic Chains Based on the Principle of Virtual Work," Proceedings of IEEE International Conference on Robotics and Automation, pp.2824-2831, 2001.
- Y. Nakamura and K. Yamane: "Dynamics Computation of Structure-Varying Kinematic Chains and Its Application to Human Figures," IEEE Transactions on Robotics and Automation, vol.16, no.2, pp.124-134, 2000.
- K. Yamane and Y. Nakamura: "Dynamics Computation of Structure-Varying Kinematic Chains for Motion Synthesis of Humanoid," in Proceedings of IEEE International Conference on Robotics and Automation, pp.714-721, Detroit, U.S.A., May 1999.
- K. Yamane and Y. Nakamura: "Dynamics Computation of Closed Kinematic Chains for Motion Synthesis of Human Figures," Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, pp.1108-1114, 1999.

| Awards | ||
| -- | 2000 Best Journal Paper of the Robotics Society of Japan | |
| -- | 2001 IEEE Robotics and Automation Society King-Sun Fu | |
| Memorial Best Transactions Paper Award |

Katsu Yamane
(Your opinions and questions about Efficient Simulation of Structure-Varying Kinematic Chains are welcome.E-mail at )
)